Ecuaciones cuadráticas sencillas

Una ecuación de segundo grado o ecuación cuadrática, es aquella en la cual la mayor potencia de la incógnita considerada en la ecuación, es dos. La expresión general de una ecuación cuadrática es

Ejemplos:

2x² + 3x = 14 

x² + 2x = 35

¿como resolverlas?

comencemos con 2x² + 3x = 14 como ejemplo.

Ensayo y error (Tanteo)

consiste en darle a x un valor cualquiera y comprobar la ecuación 

bien primero demos a x el valor de 3

2(3)² + 3(3) = 14

luego hacemos la comprobación

2(3)² + 3(3) = 14

2(9) + 9 = 14

18 + 9 = 14

27 ≠ 14

como no es igual lo debemos intentar con otro numero según el resultado en este caso 27 es mayor que 14 así que en vez de 3 podemos poner 2 y hacer la comprobación.

2(2)² + 3(2) = 14

2(4) + 6 = 14

8 + 6 = 14

14 ≡ 14

por lo tanto la respuesta correcta es 14

Por formula cuadrática

De una ecuación cuadrática con coeficientes reales o complejos existen siempre dos soluciones, no necesariamente distintas, llamadas raíces, que pueden ser reales o complejas. Se denomina fórmula cuadrática a la ecuación que proporciona las raíces de la ecuación cuadrática:

 ,

donde el símbolo ± indica que los valores

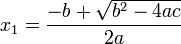
y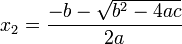

constituyen las dos soluciones.

primero cambiamos a y b por nuestros valores (aquí con 2x² + 3x = 14)

a = 2

b = 3

igualamos a 0 y hacemos las operaciones

 2x² + 3x - 14 = 0

x₁ = [-3 + √(3)² -4(2)(-14) ]/2(2)

x₁ = [-3 + √9 -4(-28)]/4

x₁ = [-3 + √9 + 112]/4

x₁ = [-3 + √121]/4

x₁ = [-3+11]/4

x₁ = 8/4

x₁ = 2

x₂ = [-3 - √(3)² -4(2)(-14) ]/2(2)

x₂ = [-3 - √9 -4(-28)]/4

x₂ = [-3 - √9 + 112]/4

x₂ = [-3 - √121]/4

x₂ = [-3-11]/4

x₂ = -14/4

x₂ = -3.5

ambos resultados son correctos tanto 2 como -3.5

Fuentes de información: Wikipedia y El evangelio según  Ramos